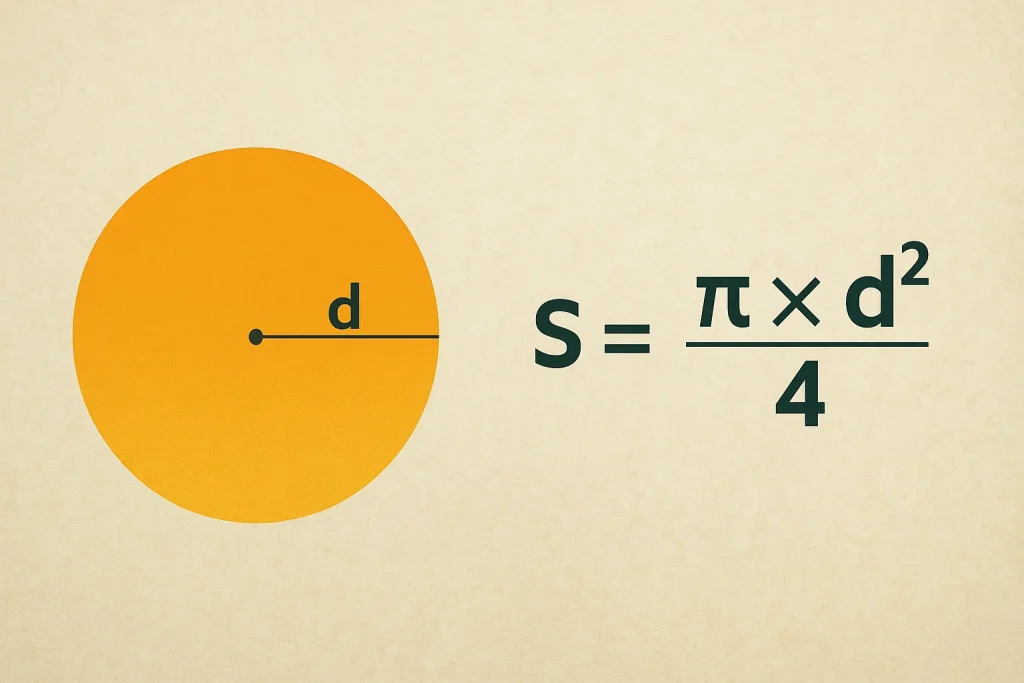Завдання знайти площу круга може здатися чимось далеким і суто шкільним, але насправді воно зустрічається в нашому житті набагато частіше, ніж можна уявити. Ремонт у квартирі, розрахунок матеріалів для клумби, кулінарні експерименти чи навіть планування розстановки меблів — усе це може вимагати знання простої, але важливої геометричної формули. На щастя, для цього не потрібно бути професором математики. Достатньо зрозуміти логіку, запам’ятати кілька ключових понять і навчитися застосовувати одну елементарну формулу. Давайте разом розберемося, як легко і швидко обчислити площу будь-якого круга.
Основи: Радіус, діаметр і таємниче число Пі (π)
Перш ніж переходити до розрахунків, важливо згадати три фундаментальні поняття, без яких неможливо зрозуміти, як знайти площу круга.
- Радіус (r) — це відстань від центра круга до будь-якої точки на його лінії (колі). Це найважливіший параметр для наших розрахунків.
- Діаметр (d) — це відрізок, що з’єднує дві точки на колі і проходить через його центр. По суті, це два радіуси, покладені на одну пряму. Тому діаметр завжди вдвічі довший за радіус: d = 2r. І навпаки, радіус — це половина діаметра: r = d / 2.
- Число Пі (π) — це магічна константа, яка зачаровувала математиків протягом тисячоліть. Вона виражає відношення довжини кола до його діаметра і є нескінченним неперіодичним дробом. Для більшості практичних розрахунків достатньо використовувати його округлене значення — π ≈ 3,14.
Розуміння цих трьох елементів є ключем до успішного розв’язання задачі.
Основна формула площі круга: знаючи радіус
Найпростіший і найпоширеніший спосіб обчислити площу круга — це використання формули, яка пов’язує її з радіусом.
S = πr²
Де:
- S — це площа круга.
- π — константа, що дорівнює приблизно 3,14.
- r² — це радіус, піднесений до квадрата (тобто, радіус, помножений сам на себе).
Простими словами: Щоб знайти площу, вам потрібно помножити число Пі на квадрат радіуса.
Приклад розрахунку
Уявімо, що ви хочете розрахувати площу круглої піци, радіус якої становить 15 см.
- Записуємо формулу: S = πr²
- Підставляємо відомі значення: r = 15 см, π ≈ 3,14.
- Спочатку підносимо радіус до квадрата: 15² = 15 × 15 = 225 см².
- Тепер множимо результат на число Пі: S = 3,14 × 225 = 706,5 см².
Отже, площа вашої піци становить 706,5 квадратних сантиметрів.
Альтернативні методи: як знайти площу, якщо відомий діаметр або довжина кола
Що робити, якщо ви знаєте не радіус, а інший параметр, наприклад, діаметр? Не біда, адже і для таких випадків існують прості формули.
Розрахунок площі через діаметр (d)
Якщо вам легше виміряти діаметр (наприклад, відстань від одного краю круглої стільниці до іншого через центр), можна скористатися модифікованою формулою.
Оскільки r = d / 2, ми можемо підставити цей вираз в основну формулу:
S = π × (d/2)² = π × (d² / 4)
S = (πd²) / 4
Порада: Щоб не заплутатися, ви можете просто спочатку знайти радіус, поділивши діаметр на 2, а потім використати стандартну формулу S = πr². Це часто буває простіше.
Приклад розрахунку через діаметр
Припустимо, діаметр круглого дзеркала дорівнює 50 см.
- Знаходимо радіус: r = 50 / 2 = 25 см.
- Використовуємо основну формулу: S = πr²
- Підставляємо значення: S = 3,14 × (25)² = 3,14 × 625 = 1962,5 см².
Площа дзеркала — 1962,5 квадратних сантиметрів.
Розрахунок площі через довжину кола (L)
Це менш поширений, але іноді корисний метод. Наприклад, якщо у вас є гнучка рулетка і вам потрібно знайти площу круглого стовпа. Довжина кола (периметр круга) обчислюється за формулою L = 2πr. Звідси ми можемо виразити радіус: r = L / (2π).
Тепер підставимо цей вираз у головну формулу площі:
S = π × (L / (2π))² = π × (L² / (4π²))
Скоротивши π, отримаємо фінальну формулу:
S = L² / (4π)
Приклад розрахунку через довжину кола
Ви виміряли довжину кола стовбура дерева, і вона дорівнює 125 см.
- Записуємо формулу: S = L² / (4π)
- Підставляємо значення: S = (125)² / (4 × 3,14) = 15625 / 12,56.
- Обчислюємо результат: S ≈ 1244 см².
Таким чином, площа поперечного перерізу стовбура становить приблизно 1244 квадратних сантиметри.
Практичні поради для точних вимірювань
Щоб ваші розрахунки були максимально точними, дотримуйтесь кількох простих рекомендацій:
- Використовуйте точне значення Пі (π). Для побутових потреб достатньо 3,14. Для більш точних інженерних чи наукових розрахунків можна використовувати 3,14159 або функцію π на калькуляторі.
- Правильно знаходьте центр. Якщо ви вимірюєте радіус, переконайтеся, що ви робите це точно від центральної точки.
- Перевіряйте одиниці виміру. Площа завжди вимірюється у квадратних одиницях (см², м², км²). Якщо радіус вимірювався в сантиметрах, то і площа буде в квадратних сантиметрах.
- Не плутайте з довжиною кола. Пам’ятайте, що площа (S = πr²) — це простір всередині круга, а довжина кола (L = 2πr) — це довжина його межі.
Знання того, як знайти площу круга, є корисним практичним навиком. Опанувавши одну просту формулу та розуміючи зв’язок між радіусом і діаметром, ви зможете легко впоратися з будь-яким завданням, де фігурує ця ідеальна геометрична фігура.